小数点 の 掛け算 なぜ 小さく なる 小数点 の 掛け算 なぜ 小さく なる
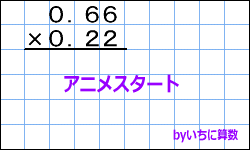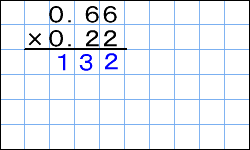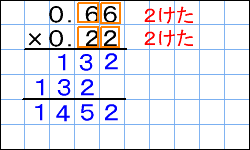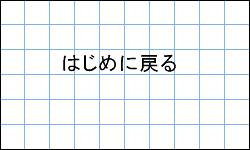
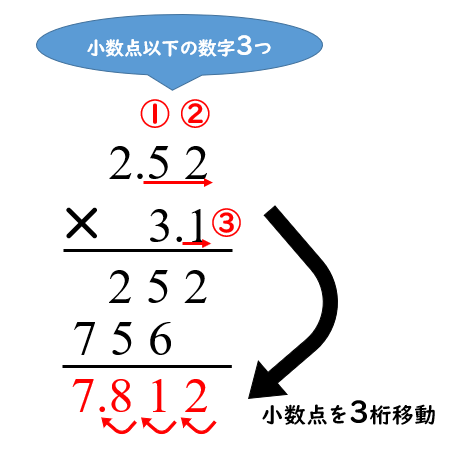
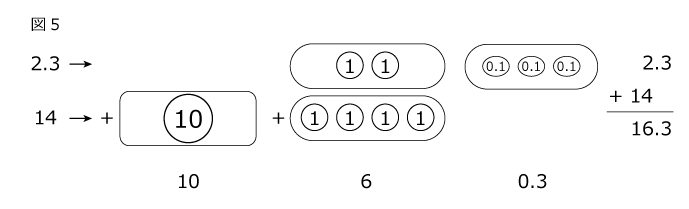
小数の掛け算の手順としては以下の通り。 小数点を無視して整数の掛け算として解く 小数点以下の桁数に応じて答えの小数点を移動させる たとえば 252× 31 252 × 31 の場合。 小数点を無視して整数として計算すると、 252× 31=7812 252 × 31 = 7812 小数点和になるようにうつよ。 積 せき の下の位 くらい が0になるとき, 小数点をうつ位 いち 置をまちがえ ないように気をつけよう。 ① 整数どうしのかけ算にするために, かけられる数を10倍する。〈位 くらい を1けた上げる〉 ② かける数も10倍する。〈位
少数 掛け算 小さくなる
少数 掛け算 小さくなる-この数直線から,答えが6より小さくなるのは 積が6より小さくなるのはどれですか 今日の学習から,積がかけられる数よりも小さくなるのはどんな時か, まとめてみましょう。 ・数直線を見ると,80よりも左側に があるので,80円より安くなります。回答時の元の質問 小数で割ると数字が大きくなることについて、子供でも分かる簡単な説明は何でしょうか? 小数というか1より小さい数ですよね。 小数なら11だって小数なので。 掛け算は「何回足すか」という演算で、例えば 3 × 2 は33を計算して
1
電卓を使っていて、いつからか小数点以下2桁が必ず表示されるようになった。 例えば100×3を計算すると写真のようになる。 このイライラをお分かり頂けるだろうか? 本日解除の仕方が分かりました! ! 嬉しすぎるので報告させて頂きます。 右上から 逆に割り算では「割ると小さくなる」という法則が定着するようです。 そのため、小数の掛け算は、小数を分数に直して 「小数の掛け算は本当は掛け算と割り算がまざっている」 ということを認識してもらうようにすれば良いと思います。 例:05×02=010変形して楽々掛け算 ところで各桁を足した数を3または9で割った時の余りが、元の数の余りになることもご存知でしたか? 入試のような限られた時間の中では効率よく正しい答えを求める方が良いので、約分して小さくしてから割り算する習慣をつけ
①その式になる理由を、説明しましょう。 ②計算の仕方を、説明しましょう。 子供に期待する解答の具体例 リボンの長さと代金は比例しているから、長さが16倍になると、代金も16倍。だから90×16になります。 21年1月24日 このページは、 小学5年生が小数の掛け算を学習するための「小数の掛け算の大小の問題集」が無料でダウンロードできる ページです。 ポイント ・整数に1より大きい小数と、1より小さい小数を掛けた時で、数が大きくなるか小さくなるかを 10×05=5 →小さくなる 10÷05= →大きくなる また更に分数では 10×1/5=2 →小さくなる 10/1/5=50 →大きくなる このように、1より小さい分数・少数の場合には、掛け算すると数は小さくなり、割り算すると数は大きくなります。
少数 掛け算 小さくなるのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 | 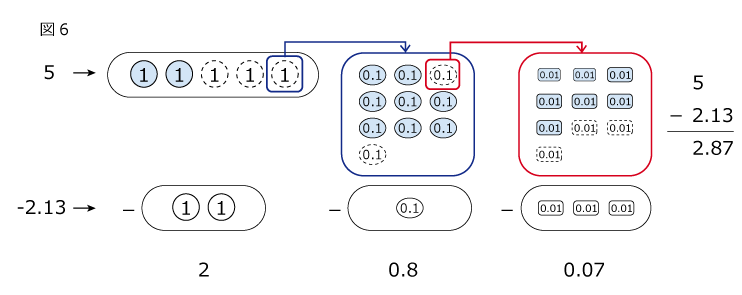 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 | 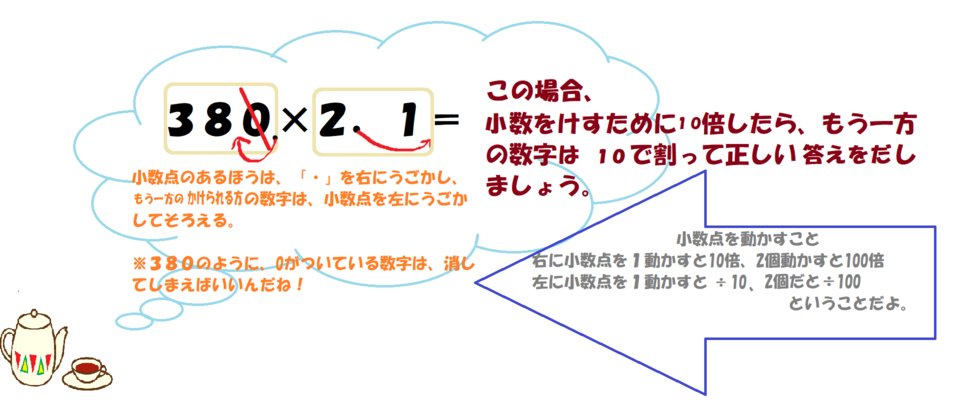 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
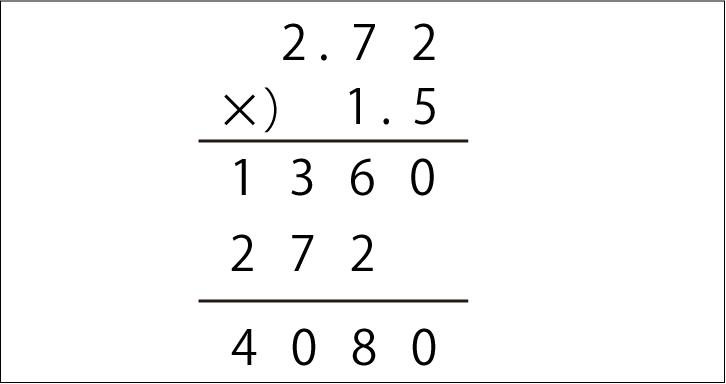 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 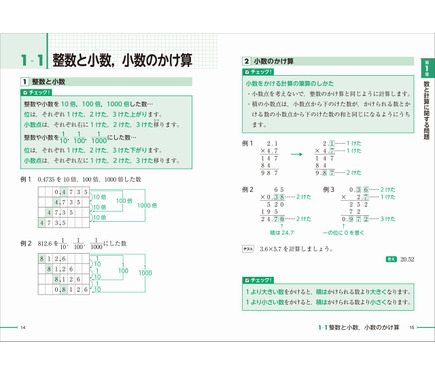 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 | 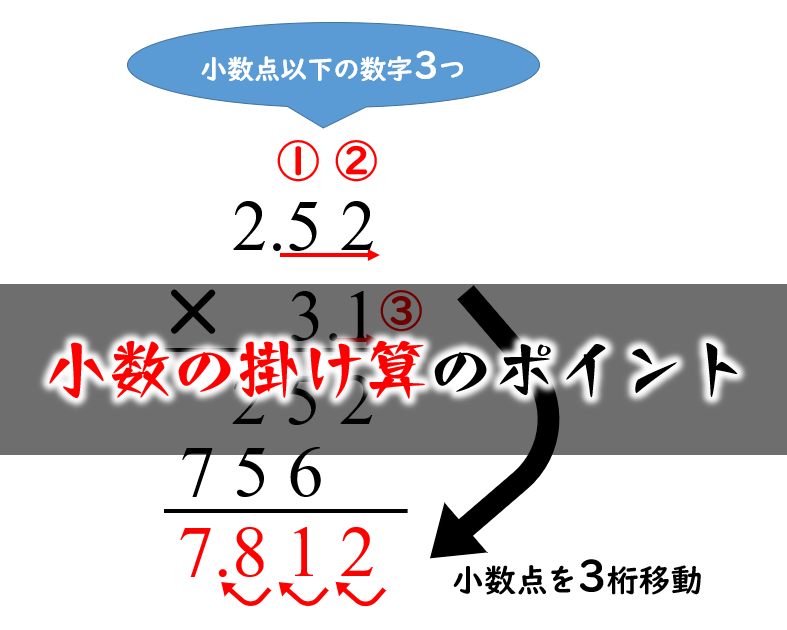 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
 算数科学習指導案 研究員研究授業用 03 | 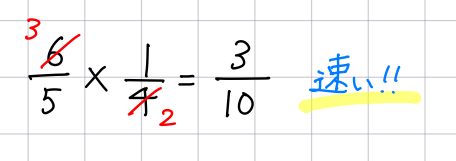 算数科学習指導案 研究員研究授業用 03 |  算数科学習指導案 研究員研究授業用 03 |
算数科学習指導案 研究員研究授業用 03 | 算数科学習指導案 研究員研究授業用 03 |
2 )商が1より小さくなる等分除「(整数)÷(整数)」 の場面で,除法が用いられることの理解に課題が ある。 1)に関する典型的な実態としては,例えば,平成 年度調査において出題された次の調大きくなるもの: ① と ② ① 6 × 12 ② 6 × 11 ③ 6 × 1 ④ 6 × 09 ⑤ 6 × 08 ・かける数が1より大きいのは ① と ② なので 答え: 1 積が6より大きくなるもの、同じもの、小さくなるものを選び、番号を 書きましょう。 ・かける数が1になるのは なので





0 件のコメント:
コメントを投稿